【笔记】主席树学习笔记
2025 CSP-S T3 中有个较为讨巧的做法:使用主席树。之前便久仰大名,却总忘了学这个东西。最近算是想起来了,也在 NOIP 之前再恶补一下。顺便看看能不能补题切除 S T3。
前置知识:权值线段树
我在 ARC210B 中,只学过经典线段树的背景下竟然想到了权值线段树,太感动了。
将数组按照其值域映射到一个线段树上,每一点表示该值出现的次数,此时该线段树就是权值线段树。
权值线段树一般要求单点修改。其进行单点修改时,仍要维护原数组。设原数组为 ${a_n}$,权值线段树为 $T$,则有:
\[ T_i=\sum_{k=1}^n [a_k=i] \]
修改 $a_x$ 并将其改为 $v$ 时,则要完成两步操作:
- $T_{a_x}\gets T_{a_x}-1$,$T_v\gets T_v+1$。
- $a_x\gets v$。
这就是为什么维护权值线段树时,也要维护原数组。
而一般权值都很大,所以在维护权值线段树时,常采用的方法是将查询离线化,再离散化,缩小数据范围并施用权值线段树。
主席树
大名:可持久化权值线段树。
分开来看各个词组的意思:
- 可持久化:保留所有历史版本。分为完全可持久化(可以修改历史版本)和部分可持久化(除了最后版本只能看不能改)。
- 权值:将改的东西映射到新数组上去做,意见上。
- 线段树:该数据结构使用线段树来维护。
其发明者是黄嘉泰。称其为主席树的原因是其名字的拼音缩写与某任主席的名字拼音缩写相同。
引入经典问题 1,洛谷 P3834。
区间 $k$ 小值问题
题目大意
给定数组 ${a_n}$,$m$ 次查询。每次查询给定 $l,r,k$。求 $a_{l\ldots r}$ 中第 $k$ 小的数。
解题思路
维护 $n$ 颗权值线段树,第 $i$ 颗树 $T_i$ 表示 $a_{1\ldots i}$ 的权值线段树。
显然,这使用了前缀和的思路,当查询 $l,r$ 时。将 $T_r-T_{l-1}$(该表示不太严谨,权当是将两颗树上每一个点的值相减),就是 $a_{l\ldots r}$ 的权值线段树。
在它上面二分,查出最早的一个点 $r$,使得 $[1,r]$ 的和不小于 $k$ 即可。
而在这个过程中,所有线段树都可以用一维的前缀和数组替代。因此,我将在后面的优化中解释为什么不使用前缀和而是采用线段树。
优化 1:空间
注意到空间复杂度 $O(n^2)$,加持大常数直接飞起来。考虑优化。
观察到每次更改需要更改的节点数是一定的——不超过树的高度,即 $\log n$。
为什么呢?因为线段树上单点修改改的一定是条链。像这个样子(图片偷自 OI-Wiki):
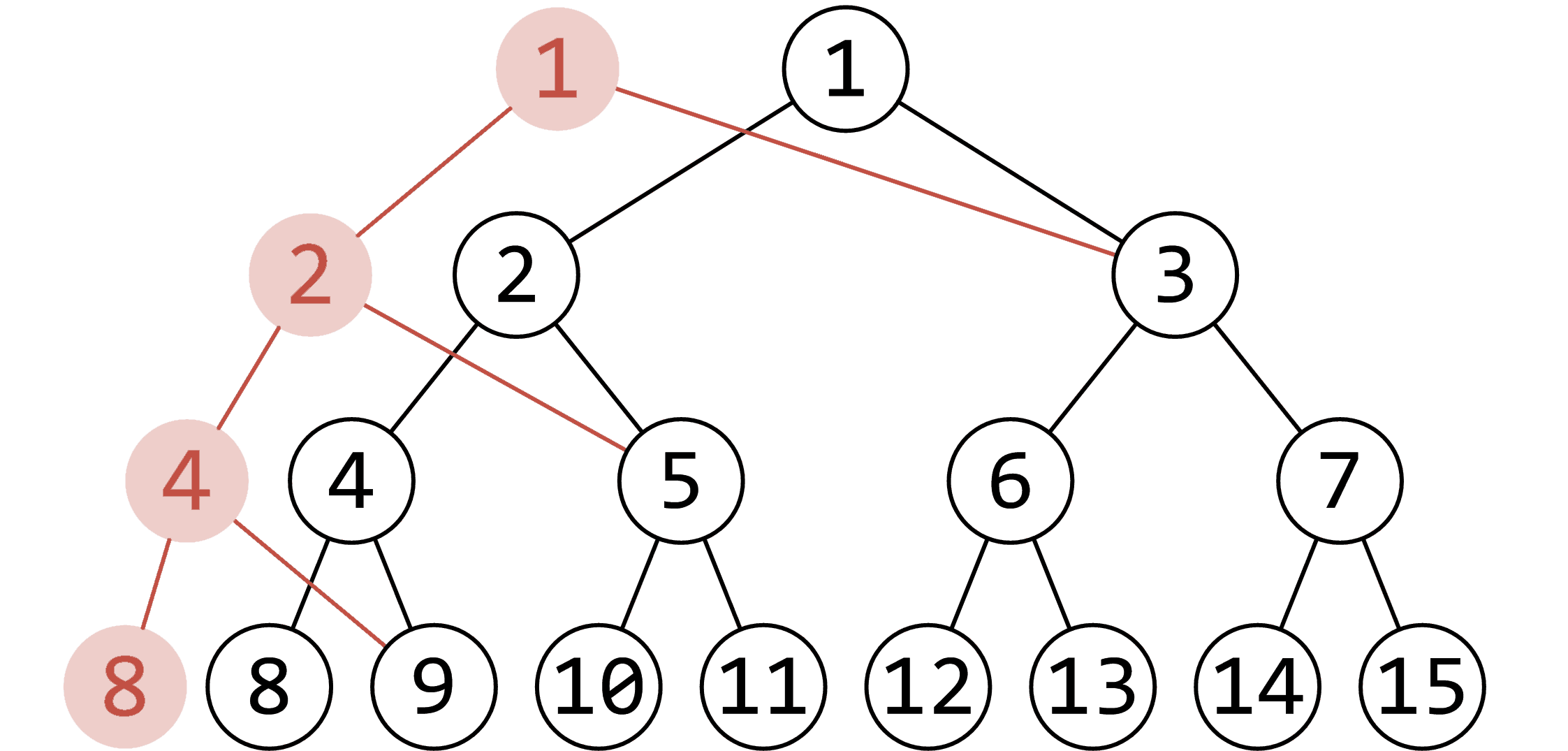
因此,使用动态开点。要用哪里开哪里。且各部分共享线段树。就是说,修改的时候,如果发现要修改的点已经有了,直接从原来的树列出来,这样每一次修改就只有 $\log n$ 的空间开销了。也就迎刃而解了。
主席树不能用 $2p$ 和 $2p+1$ 保存左右结点,而是使用计数器,开一个点加一。这个过程中,维护插入每个数时的根节点。
每次搜 $l$ 的根节点信息和 $r$ 的根节点信息,一减,做完了。主席树最多出现 $2n-1$ 个结点,因为使用的是动态开点。
最后,开数组一定要大胆,动态开点常数很大,大小开 $32n$ 甚至 $64n$ 都是可以的。一般这种题目空间都给的比较大。
优化 2:二分
如果是二分答案套上原生的线段树查询,时间复杂度还是很高的,有 $O(q\log^2 n)$。
虽然看上去对数的乘方威力不大,但 $n$ 达到一定量时,加上线段树有大常数,这个复杂度是可以飞起来的。
考虑直接在线段树上做二分:
- 如果查询值大于左树的值,搜右树,注意,在搜右树的时候,查询值要减去左树的值。
- 否则搜左树。
这样就完成了线段树上二分。复杂度降低到 $O(q\log n)$。
代码和分析
总时间复杂度:$O(n+q\log n)$。
总空间复杂度:$O(n\log n)$。
代码如下:
#include <bits/stdc++.h>
#define rty printf("Yes\n");
#define RTY printf("YES\n");
#define rtn printf("No\n");
#define RTN printf("NO\n");
#define rep(v,b,e) for(int v=b;v<=e;v++)
#define repq(v,b,e) for(int v=b;v=e;v--)
#define rrepq(v,e,b) for(int v=b;v>e;v--)
#define stg string
#define vct vector
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
void solve() {
}
const int N = 2E5 + 5;
struct ZXTree {
int l, r, val;
}tree[N * 64];
int pos[N], len, cnt, root[N], arr[N], n, m;
int getpos(int val) {
return lower_bound(pos + 1, pos + len + 1, val) - pos;
}
int build(int l, int r) {
int rt = ++cnt;
tree[rt].val = 0;
if (l == r) return rt;
int mid = (l + r) / 2;
tree[rt].l = build(l, mid);
tree[rt].r = build(mid + 1, r);
return rt;
}
int update(int l, int r, int x, int rt) {
int cur = ++cnt;
tree[cur] = tree[rt];
tree[cur].val++;
if (l == r) return cur;
int mid = (l + r) / 2;
if (x <= mid) {
tree[cur].l = update(l, mid, x, tree[cur].l);
} else {
tree[cur].r = update(mid + 1, r, x, tree[cur].r);
}
return cur;
}
int query(int l, int r, int L, int R, int val) {
int mid = (L + R) / 2;
int check = tree[tree[r].l].val - tree[tree[l].l].val;
if (L == R) return L;
if (val <= check) {
return query(tree[l].l, tree[r].l, L, mid, val);
} else return query(tree[l].r, tree[r].r, mid + 1, R, val - check);
}
main() {
cin >> n >> m;
rep(i ,1, n) {
cin >> arr[i];
pos[i] = arr[i];
}
sort(pos + 1, pos + n + 1);
len = unique(pos + 1, pos + n + 1) - (pos + 1);
rep(i, 1, n) {
arr[i] = getpos(arr[i]);
}
root[0] = build(1, len);
rep(i ,1, n) {
root[i] = update(1, len, arr[i], root[i - 1]);
}
while (m--) {
int l, r, k;
cin >> l >> r >> k;
cout << pos[query(root[l - 1], root[r], 1, len, k)] << '\n';
}
// int t; cin >> t; while (t--) solve();
return 0;
}
再引入经典问题 2:洛谷 P3919。
历史版本单点修改查询问题
题目大意
每一次操作(查询/修改)新建一个与上一版本相同的数组。第 $0$ 版本是原数组。需支持两种操作:任意历史版本的单点查询和任意历史版本的单点修改。
解题思路
可以使用主席树维护(当然可持久化数组也行)。不过这一次我们不要权值了,维护原数组即可,为什么呢?
因为在刚刚的 $k$ 小值问题中,权值法维护是因为需要求 $k$ 小值,当其转化到权值上时,要整体二分前缀和即可,否则回答所给问题会非常的麻烦。但现在只要求单点查询修改,所以用传统的线段树+动态开点+可持久化就可以完成题目要求。
这里不再讲主席树的实现了。具体来说,就是每一个新版本根据修改路径裂一个根出来,之后根据根去改就行了。
代码和分析
空间复杂度 $O(n\log n)$。
时间复杂度 $O(n\log n+q\log n)$。
#include <bits/stdc++.h>
#define rty printf("Yes\n");
#define RTY printf("YES\n");
#define rtn printf("No\n");
#define RTN printf("NO\n");
#define rep(v,b,e) for(int v=b;v<=e;v++)
#define repq(v,b,e) for(int v=b;v=e;v--)
#define rrepq(v,e,b) for(int v=b;v>e;v--)
#define stg string
#define vct vector
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
void solve() {
}
const int N = 1E6 + 5;
struct ZXTree {
int l, r, val;
}tree[N * 32];
int cnt, root[N], arr[N];
int build(int l, int r) {
int rt = ++cnt;
if (l == r) { tree[rt].val = arr[l]; return rt; }
int mid = (l + r) / 2;
tree[rt].l = build(l, mid);
tree[rt].r = build(mid + 1, r);
return rt;
}
int update(int l, int r, int x, int val, int rt) {
int cur = ++cnt;
tree[cur] = tree[rt];
if (l == r) {
tree[cur].val = val;
return cur;
}
int mid = (l + r) / 2;
if (x <= mid) {
tree[cur].l = update(l, mid, x, val, tree[rt].l);
} else tree[cur].r = update(mid + 1, r, x, val, tree[rt].r);
return cur;
}
int query(int l, int r, int x, int rt) {
if (l == r) return tree[rt].val;
int mid = (l + r) / 2;
if (x <= mid) return query(l, mid, x, tree[rt].l);
else return query(mid + 1, r, x, tree[rt].r);
}
main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, m;
cin >> n >> m;
rep(i, 1, n) {
cin >> arr[i];
}
root[0] = build(1, n);
rep(i, 1, m) {
int v, op;
cin >> v >> op;
if (op == 1) {
int p, c;
cin >> p >> c;
root[i] = update(1, n, p, c, root[v]);
} else {
int p;
cin >> p;
root[i] = root[v];
cout << query(1, n, p, root[i]) << '\n';
}
}
// int t; cin >> t; while (t--) solve();
return 0;
}

ILoveScratch
2025年11月21日 下午6:19
%%%